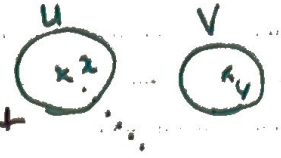Séparation, caractère T2/Hausdorff de \((E,\tau)\)
Pour tout couple de points distincts, on peut trouver un couple de
Voisinages
Ouverts disjoints. $$\forall x,y\in E,\quad x\ne y\implies\exists U,V\in\tau,\Big( x\in U,y\in V,U\cap V=\varnothing\Big)$$
- on dit que \(F\subset E\) est séparé si et seulement si \(F\) est séparé pour la Topologie induite
- la séparation se propage...
- Aux sous-ensembles
Aux topologies plus fines
Aux ensembles antécédents par une Fonction continue : $$\Big(F\text{ séparé et }\exists f:E\to F\text{ continue}\Big)\implies E\text{ séparé}$$
Aux espaces homéomorphes
- intérêt : dans un espace séparé, la Limite d'une suite est unique si elle existe
- caractérisation : \(\forall x\in E\), l'intersection de tous les Voisinages Fermés de \(x\) est égale à \(\{x\}\)
- conséquence : dans un espace séparé, les singletons sont fermés
Questions de cours
START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple de topologie séparée.
Verso: La
Topologie discrète ou la
Topologie de l'ordre.
Bonus:
END
START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple d'espace topologique non séparé mais pour lequel toute les suites convergentes admettent une limite unique.
Verso: La
Topologie co-finie et la
Topologie co-dénombrable.
Bonus:
END
START
Ω Basique (+inversé optionnel)
Recto: Expliquer pourquoi, dans un espace séparé, une suite admet au plus une limite.
Verso: Si une suite a plusieurs limites, alors ils devraient être dans des voisinages de deux points différents, qui finissent par être disjoints.
Bonus:
END